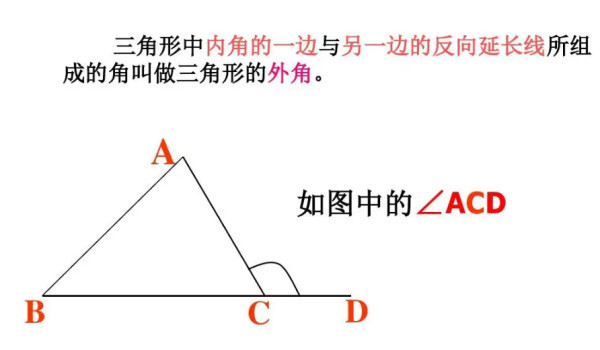
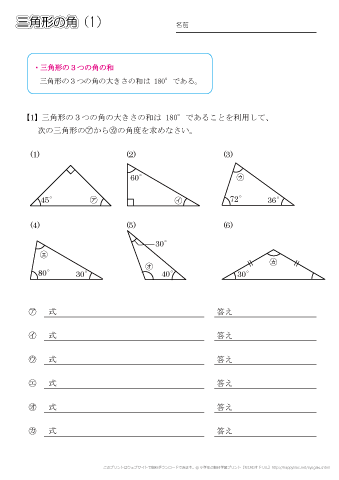
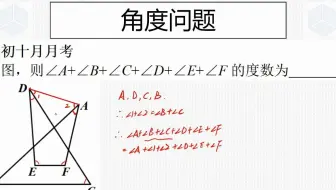
30/7/ 将多边形中已知角的度数相加,然后用总度数减去所得之和。 大多数这类几何问题是关于三角形或四边形,因为要计算的数据更少,所以我们也要这么做。 如果三角形中有两个角分别是60度和80度,相加之和是140度。 然后用三角形的角度总数,也就是180度减去
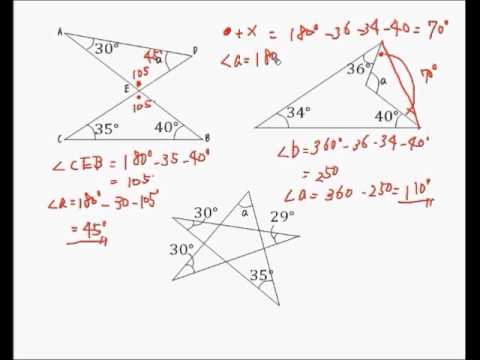
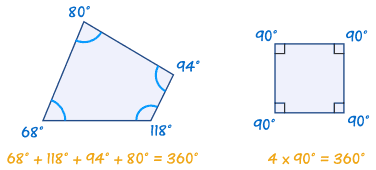
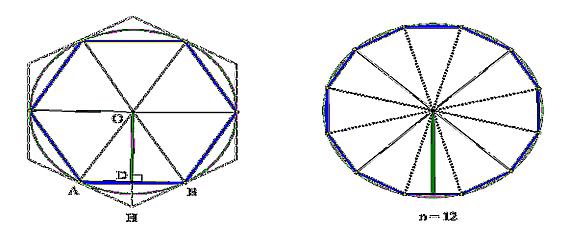
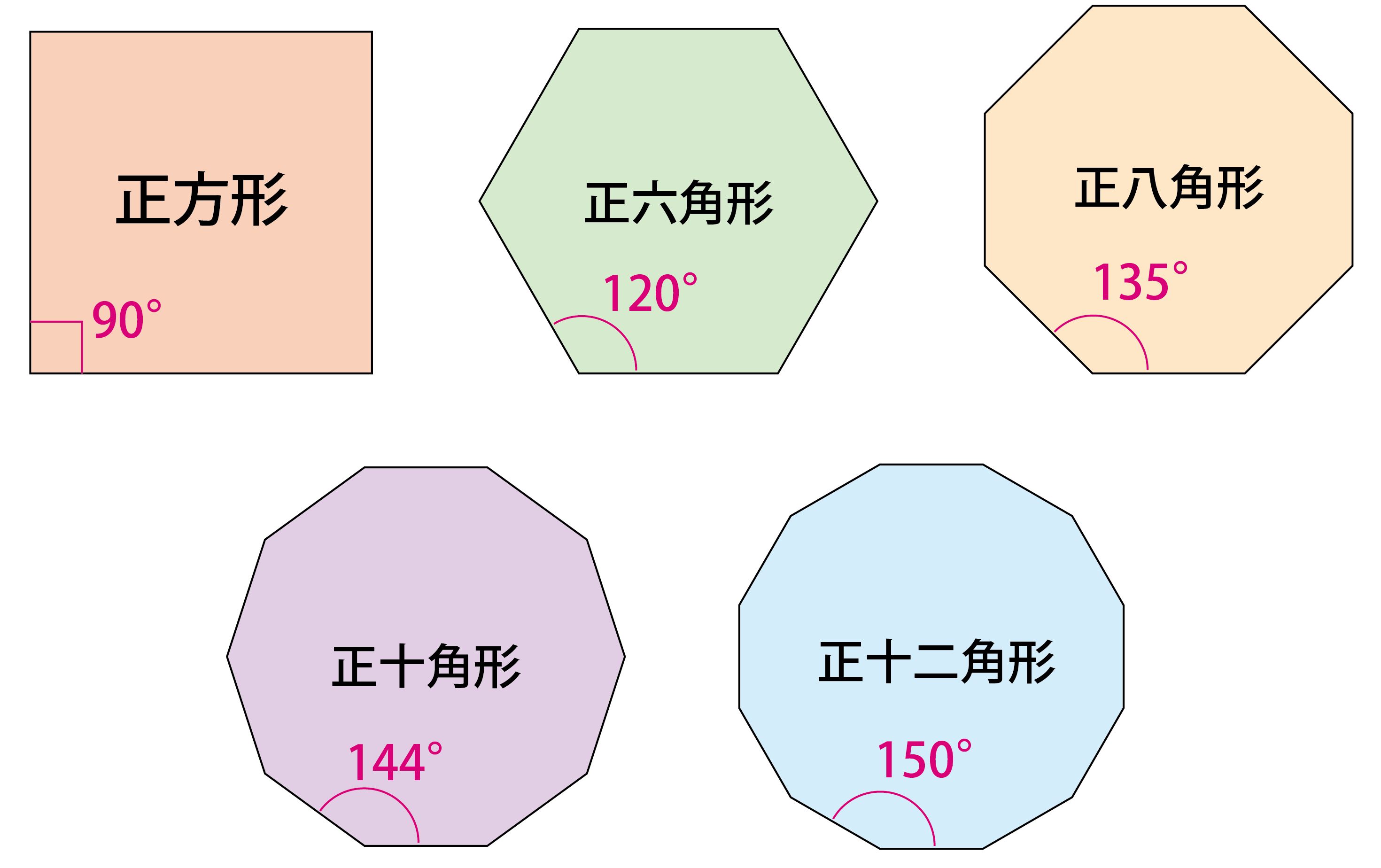
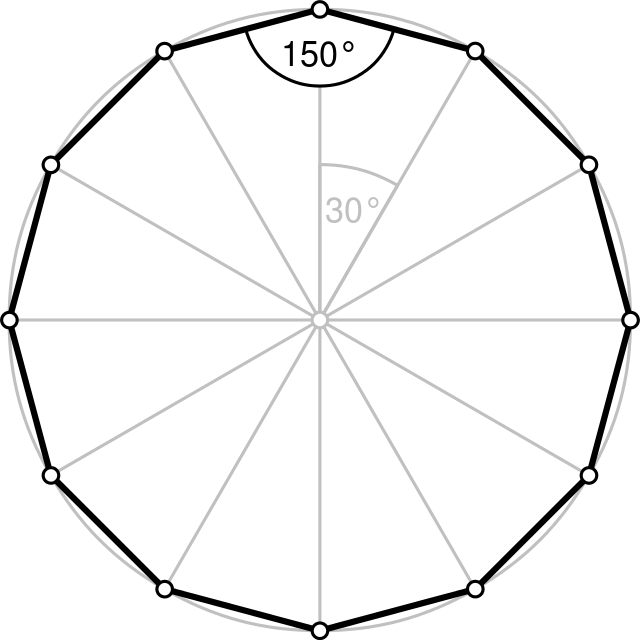
正 多 角形 角度 小5-3/8/18 多角形の性質 多角形の内角の和と対角線の数の問題です。 公式を覚えておけば出来ますが、最近は 公式の導き方 を問うことも増えています。 丸暗記するのではなく、 多角形の性質をしっかり確認して 公式を使うようにしていきましょう。2/2/21 2/5 其次,点击草图绘制按钮 3/5 之后,选择多边形工具,绘制一个六边形 查看剩余1张图 4/5 再之后,选择"智能尺寸"工具 5/5 最后,依次选中需要标注角度的角的两边即可,最终的效果如图
正 多 角形 角度 小5のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
 |  |  |
「正 多 角形 角度 小5」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「正 多 角形 角度 小5」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「正 多 角形 角度 小5」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「正 多 角形 角度 小5」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
 |  |  |
「正 多 角形 角度 小5」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「正 多 角形 角度 小5」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「正 多 角形 角度 小5」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「正 多 角形 角度 小5」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 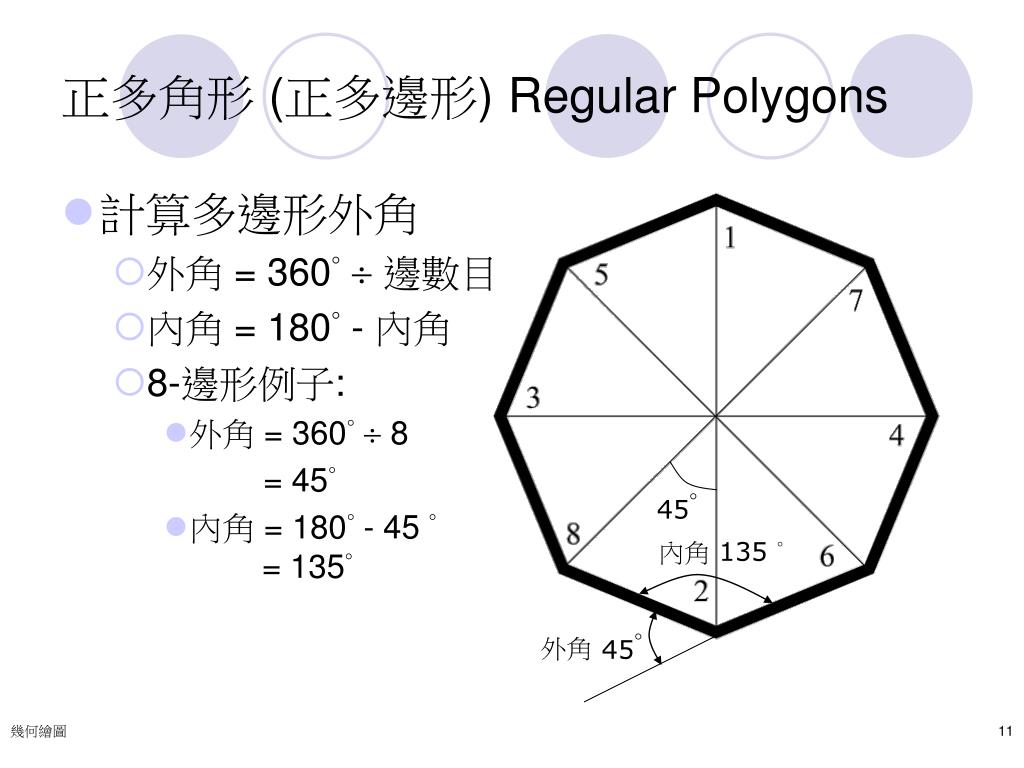 | |
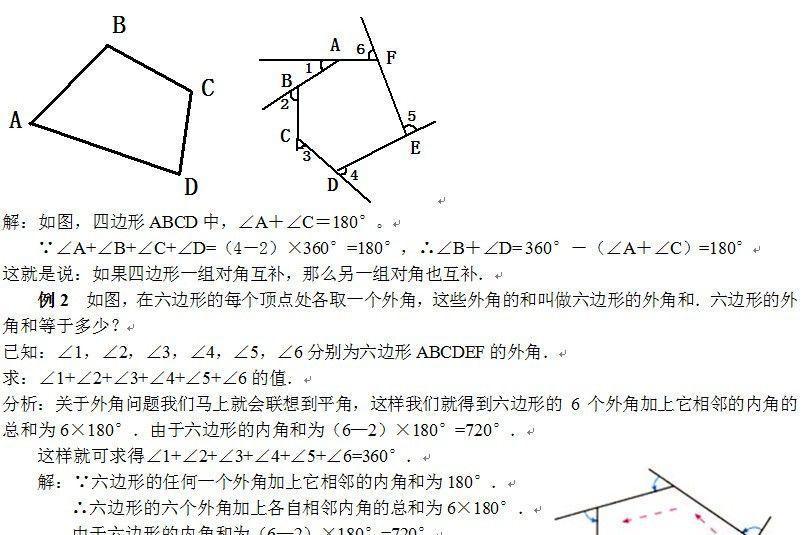
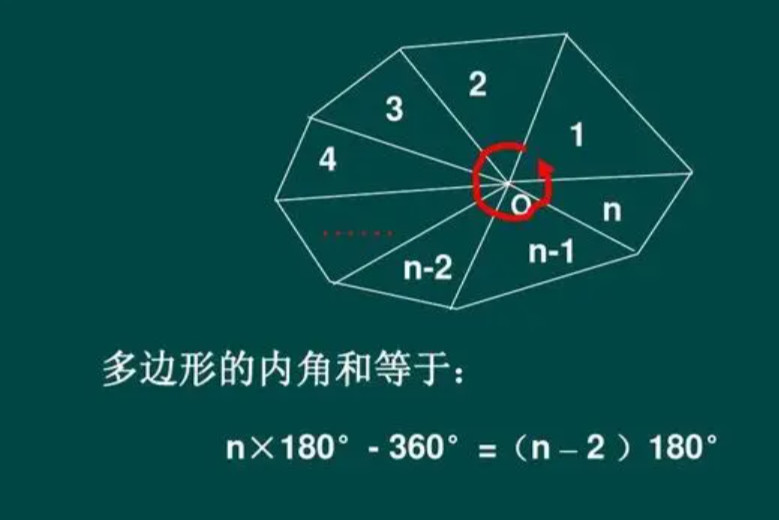
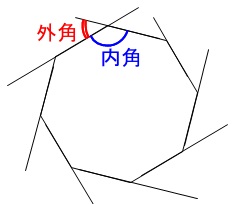
正多边形内角度数公式 ﹙n-2﹚×180°/n=180°-360°/n 180 (n2)/n 这背后的规律在于,对于二维平面上封闭曲线形成的图形,曲线一定是绕了360度回到起点。 因此,二维平面上凸多边形的外角和永远是360度。 因为显然内角和外角和=角数*180度,所以多边形内角26/1/21 前段时间有写过一个计算多边形角度的代码,这里给它整理整理,留给自己也送给萌新。看左下图,这是一个多环的多边形,一个外环(内部为多边形内部区域),一个内环(外部为多边形内部区域),同时多边形中任意一个角不等于零角(等于 0° 的角)或周角(等于 360° 的角)。
Incoming Term: 多角形 角度, 多角形 角度 公式, 正 多 角形 角度 小5,



